Solution to the inverse problem is interesting, among other reasons, for the reduction of memory space and bandwidth requirements for storage and transmission of speech signals.
Today, we’ll temporarily move away from assembly programming. It’s time to discuss a theme that I like a lot: articulatory speech synthesis. Simply put, speech synthesis comprises all the processes of production of synthetic speech signals. Currently, the most popular method for such task is the concatenative approach, which yields synthetic speech output by combining pre-recorded speech segments. Such segments, recorded from human speakers, are collected into a large database, or corpus which is segmented based on phonological features of a language, e.g., transitions from one phoneme to at least one other phoneme. A phoneme is the smallest posited structural unit that distinguishes meaning. It’s important to point out that phonemes are not the physical segments themselves, but, in theoretical terms, cognitive abstractions or categorizations of them. In turn, physical segments, referred to as phones, constitute the instances of phonemes in the actual utterances. For example, the words “madder” and “matter” obviously are composed of distinct phonemes; however, in american english, both words are pronounced almost identically, which means that their phones are the same, or at least very close in the acoustic domain.
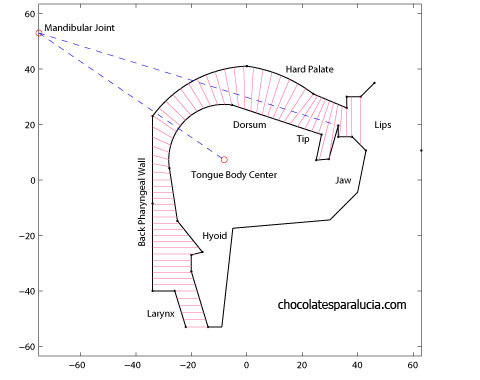
On the other hand, articulatory synthesis produces a complete synthetic output, typically based on mathematical models of the structures (lips, teeth, tongue, glottis, and velum, for instance) and processes (transit of airflow along the supraglottal cavities, for instance) of speech. Technically, articulatory speech synthesis transforms a vector p(t) of anatomic or physiologic parameters into a speech signal Sv with predefined acoustic properties. For example, p(t) may include hyoid and tongue body position, protrusion and opening of lips, area of the velopharyngeal port, and so on. This way, an articulatory synthesizer ArtS maps the articulatory domain (from which p(t) is drawn) into the acoustic domain (where frequency properties of Sv lie). Computing the acoustic properties of Sv is the task of a special function. Now, using these definitions, the speech inverse problem is stated as an optimization problem, in which we try to find the best p(t) to minimize the acoustic distance between Sv and the output of ArtS.
The solution to the inverse problem is interesting for the following applications:
- Reduction of memory space and bandwidth requirements for storage and transmission of speech signals.
- Low cost and noninvasive comprehension and recollection of data on phonatory processes.
- Speech recognition, by means of transition to the articulatory domain, where signals may be characterized by fewer parameters.
- Retrieving the best parameters for synthesis of high-quality speech signals.
However, because mapping between articulatory and acoustic domains is nonlinear and many-to-one, definition and achievement of acceptable solutions to the inverse problem are not trivial issues. Globally, qualifying a candidate solution follows some type of relation on the acoustical domain. Furthermore, from the family of solutions to the problem, we are frequently interested only in those configurations consistent to descriptions of articulatory phonetics. Several groups have approached this problem. For example, Yehia and Itakura adopted an approach based on geometric representations of the articulatory space, including spatial constraints. Dusan and Deng used analytical methods to recover the vocal tract configurations. Sondhi and Schroeter relied on a codebook technique. Genetic algorithms have also been used, albeit the approach and type of signals studied differ to those used in this research. These later studies mainly investigate relations between articulation and perception on the basis of the tasks of the task dynamic description of inputs to a synthesizer. More recent research recur to control points experimentally measured to a group of speakers, and inversion minimizes the distance between the articulatory model and the referred points, by using quadratic approximations. On our side, we have previously investigated the application of computational intelligence techniques to the speech inverse problem. Concretely, fuzzy rules for modeling the tongue kinematics, neural networks to generate the glottal airflow and genetic algorithms to carry out the overall optimization process. Another novelty of our previous research was the use of the five spanish vowels as target phonemes for inversion.
Synthesis Models
In a broader level, ArtS integrates two models: the articulatory and the acoustic model. An articulatory model represents the essential components for speech production, and its main purpose is computation of the area function A(x, t), which reflects the variation in cross-sectional area of the acoustic tube whose boundaries are located at the glottis and the mouth, respectively. Here, transitions between phonemes are not researched, and thereby the time variable will be dropped from the area function and from the vector p. On its side, an acoustic model specify the transformations between A(x) and the acoustic domain. Naturally, such mapping also requires information about the energy source exciting the tract. According to the acoustic theory of speech production, the target phonemes are considered as the output of a filter characterized by A(x) and excited by a periodic glottal signal.
In this post, we’ll restrict our presentation to the Articulatory Model:
Continue reading “Articulatory Speech Synthesis”